|
�����ł͊e�����ʑ̂̊O�ڋ��̔��a�Ɠ��ڋ��̔��a�����[�N���b�h���_�Ɋ�Â��ċ��߁A���݂̎��ۂ̘f���O�����a�̔�Ƃǂ̒��x�̌덷�����邩��������B
�i�P�j�e�����ʑ̂̊O�ڋ��̒��a
�@�j�����̂̊O�ڋ��̒��a
�@���[�N���b�h���_�@��13���@����15�ɂ�
�u�����̂�����C�^����ꂽ���ɂ���Ă����݁C�����ċ��̒��a��̐����`�������̂̕ӂ̏�̐����`�̂R�{�ł���B�v
�@�@�@�Ƃ���B�i�������A�����`�Ƃ�2��̈Ӗ��ł���B�j
�@�@�@�@
�m�ؖ��n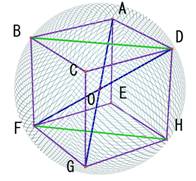
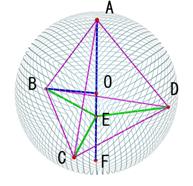
�l�p�`BFHD�ɒ��ڂ���B
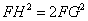 ��� ���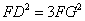
����āA
�i�����̂̈�ӂ̒����e�f�j�F�i�����̂̊O�ڋ��̒��a�e�c�j���P�F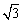
�ƂȂ�B
�A�j���l�ʑ̂̊O�ڋ��̒��a
�@�@���[�N���b�h���_�@��13���@����13�ɂ�
�@�@�@�u�p��������C�^����ꂽ���ɂ���Ă����݁C�����ċ��̒��a��̐����`���p���̕ӂ̏�̐����`�̂Q���̂R�ł���B�v
�@�@�Ƃ���B�i�������A�����`�Ƃ�2��̈Ӗ��ł���B�j
�@�@�m�ؖ��n
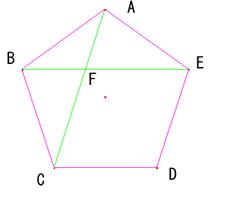
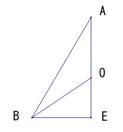 �O�p�`ABE�ɒ��ڂ���B�i�E�}�Q�Ɓj �O�p�`ABE�ɒ��ڂ���B�i�E�}�Q�Ɓj
�_E�͎O�p�`BCD�̏d�S�Ȃ̂ŁA
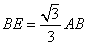 �ƂȂ�A �ƂȂ�A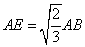 �ƂȂ�B�����ŁA �ƂȂ�B�����ŁA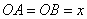 �Ƃ����A�O�p�`OBE�ɒ��ڂ���B �Ƃ����A�O�p�`OBE�ɒ��ڂ���B
����ƁA�O�����̒藝���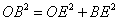 �����藧�̂ŁA �����藧�̂ŁA
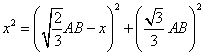 �ƂȂ�A �ƂȂ�A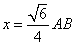 �ƂȂ�B����āA �ƂȂ�B����āA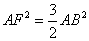 �@�ƂȂ�B �@�ƂȂ�B
����āA�i���l�ʑ̂̈�ӂ̒����`�a�j�F�i���l�ʑ̂̊O�ڋ��̒��a�`�e�j���P�F �ƂȂ�B �ƂȂ�B
�B�j�����ʑ̂̊O�ڋ��̒��a
�@�@���[�N���b�h���_�@��13���@����14�ɂ�
�@�@�u�����ʑ̂�����C�^����ꂽ���ɂ���Ă����݁C�����ċ��̒��a��̐����`�������ʑ̂̕ӂ̏�̐����`�̂Q�{�ł���B�v
�@�@�Ƃ���B�i�������A�����`�Ƃ�2��̈Ӗ��ł���B�j
�@�@�m�ؖ��n
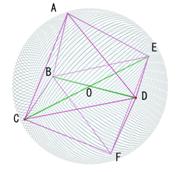
�l�p�`BCDE�ɒ��ڂ����
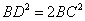
����āA
�i�����ʑ̂̈�ӂ̒����a�b�j�F�i�����ʑ̂̊O�ڋ��̒��a�a�c�j���P�F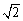
�ƂȂ�B
�C�j���\��ʑ̂̊O�ڋ��̒��a
�@�@���[�N���b�h���_�@��13���@����17�@�n�ɂ�
�@�@�@�u�����̂̕ӂ��O����ɕ�������Ȃ�A���̊O����ɕ�������Ȃ�A���̑傫�������͐��\��ʑ̂̕ӂł���B�v
�@�@�Ƃ���B�i�������A�O����Ƃ͉��������̈Ӗ��ł���B�j
�@�@�m�ؖ��n
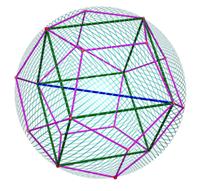 ���\��ʑ̂̒��ɂ͍��}�̂悤�ɗ����̂������Ă���B���̗����̂̈�ӂ̒����͐��\��ʑ̂̐��܊p�`�̑Ίp���̒����ƈ�v���Ă���B ���\��ʑ̂̒��ɂ͍��}�̂悤�ɗ����̂������Ă���B���̗����̂̈�ӂ̒����͐��\��ʑ̂̐��܊p�`�̑Ίp���̒����ƈ�v���Ă���B
�܂�A�}3��BE�̒��������\��ʑ̂ɓ��ڂ��闧���̂̈�ӂ̒����ɂȂ�B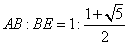 �i�O�p�`AFB�ƎO�p�`EAB�̑����𗘗p���ċ��߂���B�j�����藧�B �i�O�p�`AFB�ƎO�p�`EAB�̑����𗘗p���ċ��߂���B�j�����藧�B
����āA����AB�̒����͐���BE�̒��������������������̑傫�������̒����ɂ����邱�Ƃ�������B
 ����ɁA���̗����̂̑Ίp���̒����͐��\��ʑ̂̊O�ڋ��̒��a�ɂ������Ă���̂ŁA��ӂ̒�����������A���\��ʑ̂̊O�ڋ��̔��a��������B ����ɁA���̗����̂̑Ίp���̒����͐��\��ʑ̂̊O�ڋ��̒��a�ɂ������Ă���̂ŁA��ӂ̒�����������A���\��ʑ̂̊O�ڋ��̔��a��������B
������A�i���\��ʑ̂̊O�ڋ��̒��a�j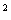 �� ��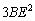 �@ �@
��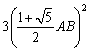 �ƂȂ�B �ƂȂ�B
�@�@�@�@�@�@�}3
�@�@����āA
�i���\��ʑ̂̈�ӂ̒����`�a�j�F�i���\��ʑ̂̊O�ڋ��̒��a�j���P�F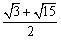 �ƂȂ�B �ƂȂ�B
�D�j����\�ʑ̂̊O�ڋ��̒��a
�@�@���[�N���b�h���_�@��13���@����16�̌n�i�v��j
�@�@�@�u����\�ʑ̂��ォ�猩���Ƃ��̐��܊p�`�̊O�ډ~�̔��a��2�悪����\�ʑ̂�
�O�ڋ��̒��a��2���5����1�ɓ������B�v
�@�@���[�N���b�h���_�@��13���@����10�i�v��j
�@�@�@�u���܊p�`���~�ɓ��ڂ��Ă���Ƃ��A���̐��܊p�`�̕ӂ�2��͓����~�ɓ��ڂ���
���Z�p�`�̕ӂƐ��\�p�`�̕ӂ�2��̘a�ɓ������B�v
�@�@
�@�@�̓���琳��\�ʑ̂̈�ӂ̒����ƊO�ڋ��̒��a�Ƃ̊W���������B
�@�@�m�ؖ��n�i���[�N���b�h���_�@��13���@����16�̌n�j
�@�@�@
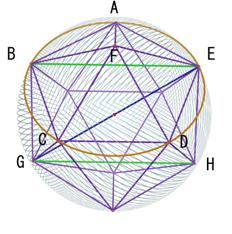
���\��ʑ̂̐����̂Ƃ���ł�����悤�ɁA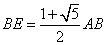 �A �A ��� ���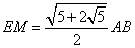 ��������B ��������B
�O�p�`EBM�ƎO�p�`ENB�̑����𗘗p����Ɓ@�@�@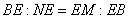
��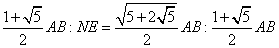
��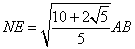 �ƂȂ�B �ƂȂ�B
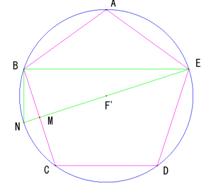 ����āA���܊p�`ABCDE�̔��aEF�f�� ����āA���܊p�`ABCDE�̔��aEF�f��
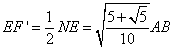 �ƂȂ�B����A����\�ʑ̂̒� �ƂȂ�B����A����\�ʑ̂̒�
�a�ł���EG�̒����͒����`BGHE�ɒ��ڂ��邱�Ƃɂ���Ăł���B
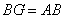 �� ��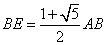 �ƂȂ�B �ƂȂ�B
����āA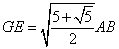 �ƂȂ�B �ƂȂ�B
�ȏ���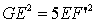 �����藧���Ƃ��������B �����藧���Ƃ��������B
�@�@�m�ؖ��n�i���[�N���b�h���_�@��13���@����10�j
�@���̖���ŏq�ׂĂ��鐳�Z�p�`�̈�ӂ̒�����EF�f�ɑ�������B�܂��A���\�p�`�̈��
�̒����̓��[�N���b�h���_�̑�P�R���̂T����тX���EF�f�����������������̑傫������
�̒����ł���B
�܂�A �ƂȂ��Ă���B �ƂȂ��Ă���B
������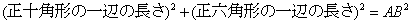 ���������B ���������B
�ȏ���
�@�@�i����\�ʑ̂̈�ӂ̒���AB�j�F�i����\�ʑ̂̊O�ڋ��̒��aEG�j���P�F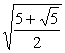 �ƂȂ�B �ƂȂ�B
�i2�j�e�����ʑ̂̓��ڋ��̔��a
�J���p�k�X�ł̃��[�N���b�h���_�̑�P�T���̍Ō�̖���ł́A�u���̐}�`�̒��S�Ɗ��ʂ̒��S�����Ԓ����͓��ڋ��̔��a�ł���v�Ƃ���B
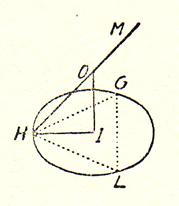 ���}�̏ꍇ�AOI�����ڋ��̔��a�ɂ����邪�A�O�p�`OHI�ɒ��ڂ��āA�O�����̒藝���g���Β����ɋ��߂���BOH�̒����͐����ʑ̂̊O�ڋ��̔��a�ƈ�v���AHI�̒����͊��ʂ̊O�ډ~�̔��a�ƈ�v���Ă���B�O�ڋ��̔��a�ɂ��Ă͂������łɋ��߂Ă���̂ł��Ƃ́A���ʂ̊O�ډ~�̔��a�����߂�Ηǂ��B ���}�̏ꍇ�AOI�����ڋ��̔��a�ɂ����邪�A�O�p�`OHI�ɒ��ڂ��āA�O�����̒藝���g���Β����ɋ��߂���BOH�̒����͐����ʑ̂̊O�ڋ��̔��a�ƈ�v���AHI�̒����͊��ʂ̊O�ډ~�̔��a�ƈ�v���Ă���B�O�ڋ��̔��a�ɂ��Ă͂������łɋ��߂Ă���̂ł��Ƃ́A���ʂ̊O�ډ~�̔��a�����߂�Ηǂ��B
�T�̐����ʑ̂̊��ʂ̌`�͐��O�p�`�A�����`�A���܊p�`�̂R��ނ����Ȃ��B��{�I�ɂ͐����藝��p���邱�Ƃɂ���ċ��܂�B
�i�@�j���ʂ����O�p�`�̏ꍇ�@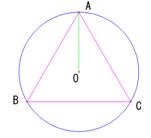
�O�p�`ABC�ɐ����藝��p�����
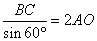
�ƂȂ�B
�i�A�j���ʂ������`�̏ꍇ
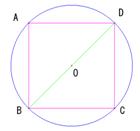
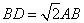
�ƂȂ��Ă���B
�@
�i�B�j���ʂ����܊p�`�̏ꍇ
�@�@���܊p�`�̊O�ډ~�̔��a�ɂ��Ă͐���\�ʑ̂̊O�ڋ��̔��a�����߂�Ƃ��ɂ���
���łɋ��߂Ă���B���܊p�`�̈�ӂ̒�����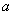 �Ƃ����� �Ƃ�����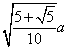 �ƂȂ�B �ƂȂ�B
�i3�j���ۂ̘f���O�����a�̔�Ƃ̔�r
�@
|
|
�O�ڋ��̔��a
|
���ڋ��̔��a
|
�O�ڋ��Ɠ��ڋ��̔��a�̔�̒l
|
���ׂ݂̗荇���f���O�����a�̔�̒l
|
|
������
|
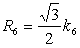
|
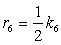
|
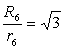
|
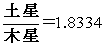
|
|
���l�ʑ�
|
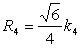
|
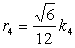
|
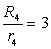
|
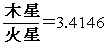
|
|
�����ʑ�
|
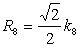
|
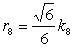
|
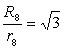
|
|
|
���\��ʑ�
|
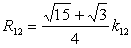
|
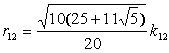
|
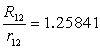
|
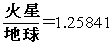
|
|
����\�ʑ�
|
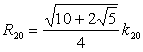
|
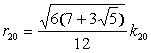
|
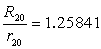
|
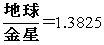
|
�@�@�@�@���������A �͊e�����ʑ̂̈�ӂ̒�����\���Ă���B �͊e�����ʑ̂̈�ӂ̒�����\���Ă���B
�@
�@�@���̕\���P�v���[�̉F���͌^���\���f���O�����a�̔�̒l�Ǝ��ۂ̘f���O�����a�̔�
�̒l�Ƃ͋߂��悤�ʼn����l�ƂȂ��Ă��邱�Ƃ�������B
|