 |
箱庭の原理 |
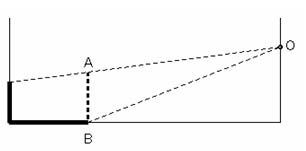
視点をOとし、これを箱庭における穴とします。太い線で書かれているのが、箱庭において実際に描かれている図です。このOから中をのぞくと四角錐が見えるのは、太い点線で描かれているABという図が、手前にあるように見えるからです。すなわち、箱庭の側面と底面に描かれている図は、箱庭中央に存在しているように見える四角錐を箱庭に投影した投象になります。
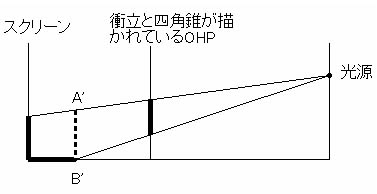
この箱庭の仕組みを光と影を使って体験できるのが、「どんなふうに使うのかな?」でも紹介されている、装置を使っての実験です。下の図は、その装置の模式図です。上の図と違うのは投影する四角錐がOHPに描かれているということです。この四角錐をスクリーンに投影することで、箱庭において実際に描かれている図ができます。つまり、上の図と同じように、光源の位置から見ると、スクリーンに描かれている図は四角錐に見え、さらに手前のOHPに描かれている四角錐と重なります。ちなみに太い点線で描かれているA’B’は、OHPがない場合には、上の図と全く同じ役割をします。さらにA’B’とOHPに描かれている図は相似な関係になります。 |
 |
正方形を拡大する活動についての数学的説明 |
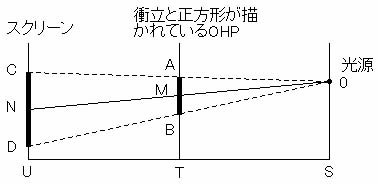
| 衝立とスクリーンは互いに平行を保っています。すなわち、影の大きさを変えるためにスクリーンを動かすとき、必ずこの関係を保ったまま動かすことになります。図において、AB//CDのとき、同位角は等しいので、∠OAB=∠OCD、∠OBA=∠ODCより、2組の角が等しいので、△OAB∽△OCDと言えます。よって、相似な図形の対応する辺の比は等しいので、OA:OC=AB:CD。今、OからUTに垂直な線を引き、その交点をSとすると、平行線と線分の比の定理から、OA:OC=ST:SU。以上から、AB:CD=ST:SUが言えます。つまり、OHPに描かれている正方形とスクリーンに投影される正方形の大きさの関係は、光源から衝立までの距離と光源からスクリーンまでの距離に依存することが分かります。影の大きさをもとの図の2倍に拡大したいときは、光源から衝立までの距離の2倍の位置にスクリーンを置けばいいことになります。 |
|