零約術は不尽数を簡単な分数で表すための術である。これは、関孝和によって創められたものである。零約という単語も関孝和の拾遺諸約、括要算法等に始めて見られる。関の零約術は、後の和算家の零約術とは大きく異なる。関の零約術は一種の平均法によって次第に真の値に近づけていくものである。しかし、大成算経に書かれている零約術はこれとは大きく異なり、連分数と同一の理論に基づいている。大成算経は関の晩年に、高弟建部賢弘・賢明兄弟の助力のもと、関の研究を纏め上げた書物である。したがって、建部兄弟の考えが加えられていることは明確であり、どこまでが関の研究でどこからが建部兄弟の研究であるかは不確かである。しかし、綴術算経のなかで賢弘がいうには、この零約術は兄賢明の創案であると主張している。
　大成算経の零約術は不尽数を連分数に展開し、その近似分数を不尽数として扱うというきわめて近代的なやり方である。しかし、この計算方法は、和算特有の両一術，翦管術が用いられている。これらの術の中にも連分数の理論が見られる。特に、建部の累約術にいたってはこの連分数の理論がより一層活用されている。これらの研究から大成算経の零約術を生み出し、他の和算家の研究によって零約術は発展していった。

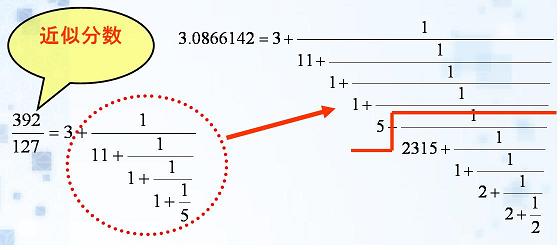
大成算経で用いられる零約術は連分数の考えを元に近似を行っている。両端に現れる段の数字を用いて、下の図のように連分数を作っている。3.0866142であれば5つの数字まで取り出しているので第五率（第五弱率）まで求めていることになっている。