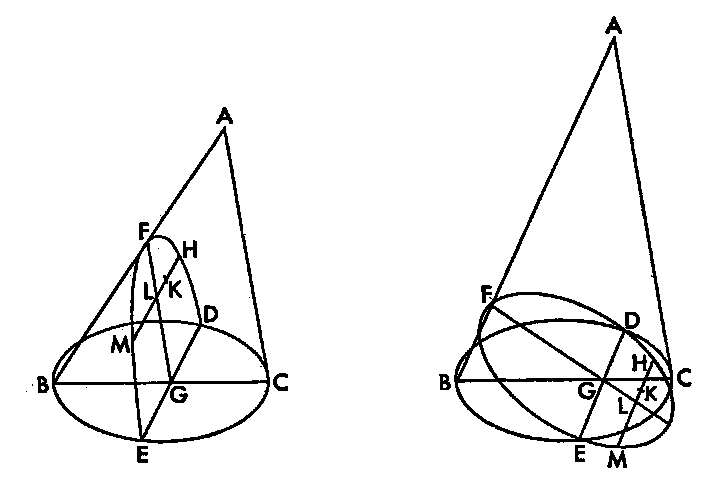命題7:円錐が軸を通る平面で切断され、軸三角形の底辺やそれを延長したもののいずれかに垂直な直線を含み円錐の底面を切断する別の平面でも切断されるなら、円錐の表面上のその結果の切断面から引かれた切断によってできた三角形の底辺に垂直な直線に平行な直線は、切断平面と軸三角形の共通部分に下ろされる。そして、切断面の別の側に延長すると、共通部分で二等分される。そして、もし直円錐なら底面の直線は切断面と軸三角形の共通部分に垂直になり、斜円錐なら軸を通る平面は常に垂直とは言えないが、軸を通る平面が円錐の底面に垂直な時はいつでも垂直である。
頂点がAで、円BCを底面とする円錐がある。それを軸を通る平面で切断し、切断面として三角形ABCを作る。(Ⅰ.3)円BCのある平面を別の平面でも切断し、直線DEを含み直線BCかそれを延長したもののいずれかに垂直で、円錐の表面の切断面として曲線DEFを作る。
すると、直線FGは切断面と三角形ABCの共通部分である。そして、任意に点Hを切断面DEF上にとり、直線HKをHを通り、直線DEに平行に引く。直線HKはFGと交わり、切断面DEFの反対側に延長されるなら、FGによって二等分されるだろう。