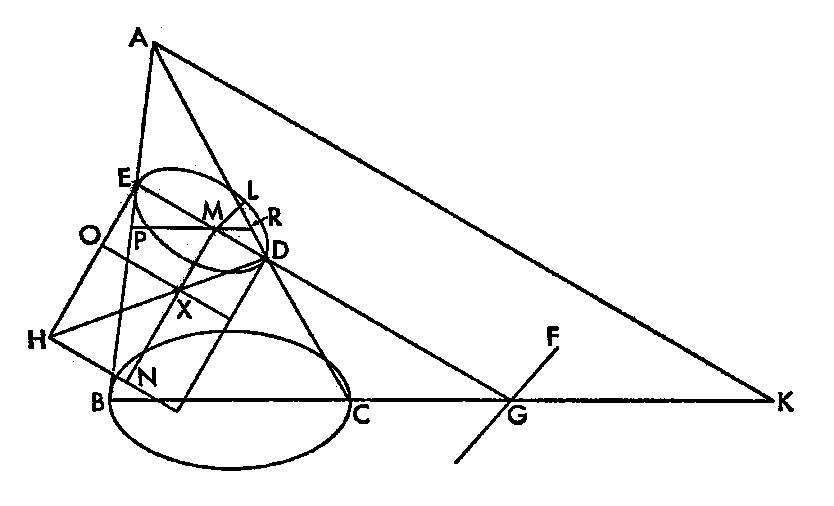
命題13:円錐がその軸を通る平面によって切断され、一方では三角形の両側で交わり、他方では底面に平行でも小反対断面でもなく延長された別の平面で切断され、円錐の底面がある平面で切断面が軸三角形の底辺かその延長されたものに垂直な直線と交わるなら、円錐の切断面から平面の共通部分に平行に切断面の直径に引いたどんな直線も平方は、切断面の直径が円錐の頂点から三角形の底辺に切断面の直径に平行に引いた直線上の平方が(底辺上の)三角形の辺から切り取るこの直線で挟まれる矩形に対する比を持ち、幅として切断面の頂点からはじまる直径を切断面から直径までの直線によって切り取る直線を持ち、直径とパラメーターで挟まれる矩形と相似で同様な図形だけ不足して直線にあてはまるある面積に等しい。そしてそのような切断面を楕円という。
頂点が点Aで、底面が円BCである円錐がある。軸を通る平面で切断し、切断面として△ABCをつくる。一方では軸三角形の両辺と交わり、他方では円錐の底面にも小反対断面にも平行でなくひろがった別の平面でも切断する。円錐の表面上の切断面としてDEを作りとする。切断面と円錐の底面のある平面の共通部分が直線BCに垂直な直線FGであるとする。切断面の直径は直線EDである。(ユークリッド.Ⅰ.7,と定義4)直線EHはEを通りEDに垂直に、直線AKはAを通りEDに平行に引く。AK2:BK・KC=DE:EH となるように工夫する。切断面上に任意の点Lをとり、直線LMはLを通りFGに平行に引く。
直線LMの平方が幅としてEMを持ち、DEとEHで挟まれた矩形に相似な図形だけ不足してEHにあてはまる面積に等しい。