| 3.もう少し詳しい各図の説明 |
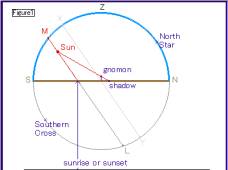 |
| Figure1の円は天球を真西の方向から見たところを表しており“N”,“S”,“Z”,“North Star(北極星)”,“Southern Cross(南十字星)”の5点はそれぞれ,天球上の北点,南点,天頂,北極,南極にあたります。そして中心を通るXYは天の赤道を表し,XYに平行なMLで太陽の運行を真横から見たところを表します。よってMLと地平線NSとの交点は日の出・日の入りの位置になります。またこの円は子午線に相当し,点Mが太陽の南中する位置となります。地平線上に立てられたノーモンの,太陽光による影の先端を点“shadow”で表していますが、これは太陽からノーモンの先端に向けて放った半直線と地平線NSとの交点です。 |
|
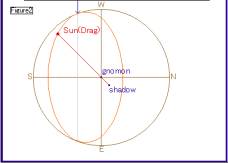 |
| Figure2の円は天球を天頂(Figure1内では点Z)の方向から見たところを表しており,Figure1と対応しています。円は地平線を表し,中心はノーモンの位置,そして4点“E”,“W”,“S”,“N”で東西南北を表しています。この図内では太陽の運行は楕円で表されていますが,円と楕円との接点が日の出・日の入りの位置になります。“Sun(Drag)”はドラッグすることができるので,太陽の位置と影の先端“shadow”との関係をFigure1と対応させながら見てみてください。CabriJavaのトレース機能を用いて“shadow”の軌跡を描くと,影のでき方がよくわかります。 |
|
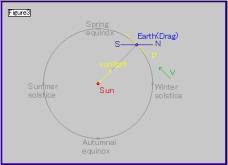 |
| Figure3は地球の公転軌道を表したもので,円軌道として理想化し,作図してあります。円上の4つの点は右方から半時計回りに冬至,春分,夏至,秋分にあたり,地球を通る黄色の線分P(接線方向)は地球を昼側と夜側に二分する平面を表しています。線分NSは,地軸の公転面への正射影として捉えてください。また,歳差運動は考慮していません。“Earth(Drag)”はドラッグすることができます。線分NSと線分Pとの位置関係を,Figure4における地軸NSと黄色の線分Pとの位置関係と比較しながらドラッグしてみてください。 |
|
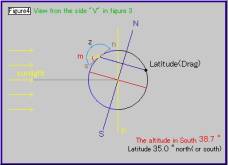 |
Figure4は太陽方向への地軸の傾きを表したもので,Figure3内の“V”の側から地球をみた様子を表しています。正確には,地球を昼側と夜側に二分する平面Pと赤道面との交線の方向からみた様子ということになります。Figure3と同様,黄色の線分Pが昼側と夜側を二分する平面を表し,この平面と地軸とのなす角度をFigure3を用いて計算しています。
地球に接している小さな半球はFigure1との関連をイメージしやすくするためにつくりました(mが南中位置の方向です。)“Latitude(Drag)”をドラッグすることで観測点の緯度を変えることができます。Figure1,Figure2と照らし合わせながらドラッグしてみてください。(ただしこのドラッグとFigure1,2内の太陽の位置(点“Sun”または“Sun(Drag)”の位置)とは対応していません。) |
|



