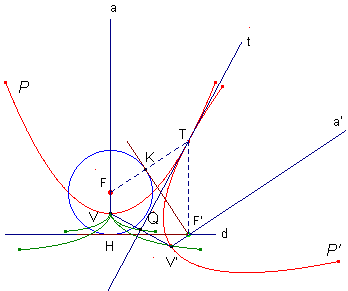
放物線Ｐ上の点Ｔ(任意)における接線について対称な放物線Ｐ'がある。このとき、放物線Ｐ’の焦点Ｆ’は常に放物線Ｐの準線 d 上に存在する。
実際、点Ｆ’は接線ｔについて放物線Ｐの焦点Ｆと対称で TF=TF' となるからこの接線 ｔ は ∠FTF'の二等分線であり、直線 TF'は放物線Ｐの準線 ｄ に垂直である。放物線Ｐの軸 a は直線F'Tと平行であり、放物線Ｐ’の軸 a' は直線FTと平行となる。
点Ｆから(準線ｄへ)おろした垂線の足Ｈまでの距離(FH)は一定で、点Ｆ’から軸 a' に垂直な直線を伸ばし、FTとの交点をＫとすると線分FKは一定(FK=FH)となる。
直線F'Kは常に中心Ｆ、半径FHの円周に接し、点Ｑは直線 t 上にあって、２つの放物線の頂点を結ぶ線分は放物線Ｐの点Ｖに関するpodaria(垂足)であり、この点Ｑは cissoide (ｼｯｿｲﾄﾞ) を描く。
点Ｖ’はすべての位置についてこの曲線(ｼｯｿｲﾄﾞ)とomotetia 同相で(点Ｑに依存して位置は決まるのだが)点Ｖを中心としたＶからの距離の比が２倍のcissoide (ｼｯｿｲﾄﾞ)となる。