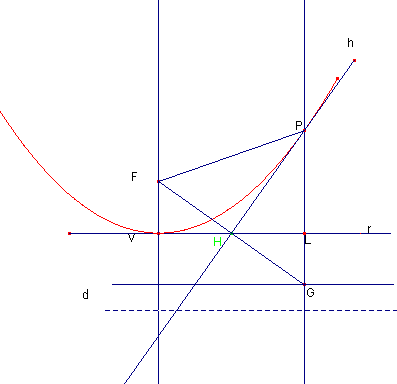
包絡線の作り方について。点Ｆおよび(Ｆを通らないように)外側に直線 r をおく。直線 r 上に点Ｈをとり、この点ＨでＦＨに垂直な直線 hを引く。 このとき、 直線 h による包絡線が放物線であることを示そう。
点 G を点Ｈに関して点Ｆに対称にとる。このとき、直線 GP は直線 r に垂直となる。よって、 PF=PG
また △FVH ≡ △HLG より LG=VF となるから、点Ｇと直線 r との距離は一定。
従って、点Ｆと直線 r との距離に等しい距離だけ離れた(直線 r に平行な)直線 d 上に点Ｇはある。
以上から、点Ｐは点Ｆと直線 d から等距離にあるので、焦点Ｆ、準線 d の parabola放物線上にある。
また、このとき ∠ FPH = ∠HPG となるから直線 h は点Ｐを接点とする放物線の接線となる。