Dimostrazione
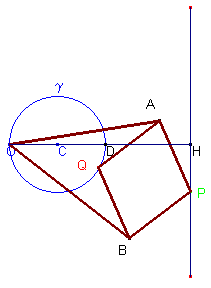
２点Ｐ，Ｑは反転装置 OAPBQ によって対応する点である。 「点Ｐが点Ｏを通る円を描くとき、点Ｑは直線 s を描く」というこの対応(変換)の特徴 (proprietà della inversione circolare反転図形の性質) により、「点Ｐが(Ｏを通らない)直線 s を描くとき、点Ｑは点Ｏを通る円を描く。このときの円の中心はＯを通り直線 s に垂直な直線上にある。」このことは明らかである。 また、点Ｏから直線 s に引いた垂線の足をＨとおく。 さらに　　 , 　　　　 　　とおく。 すると、(D と H は反転図形であるから)　　2r ・ d = a2 − b2　 この関係式により、円 g の半径 r を決めることができる。