La podaria di una parabola rispetto al suo vertice è una cissoide.
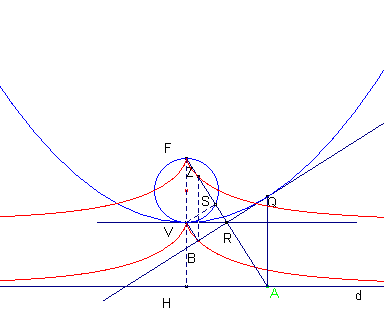Siano F e d rispettivamente fuoco e direttrice di una parabola P . Sia Q il punto di intersezione dell'asse del segmento FA con la perpendicolare a d condotta per A : quando A percorre d, Q descrive la parabola P e la QR (R punto medio di FA) è tangente alla parabola in Q.
Siano:
- B il piede della perpendicolare condotta dal vertice V della parabola a tale tangente.
- S il punto di intersezione della FA con la circonferenza di diametro FV.
- Z il punto di intersezione della parallela ad FH (tracciata per B) con FA.
I triangoli FSV e ZRB son uguali, quindi ZR=FS. Z descrive allora una cissoide C. Essendo BZ=VF, B è il corrispondente di Z nella traslazione individuata dal vettore FV quindi descrive la cissoide traslata della C.