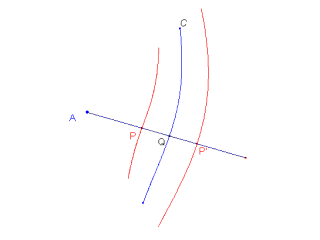
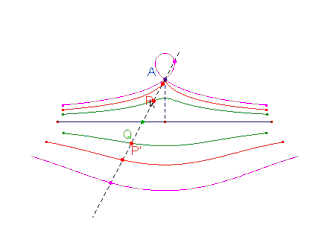
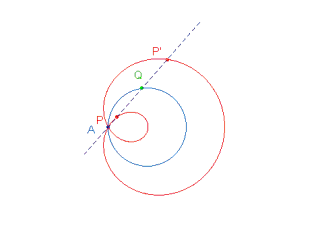
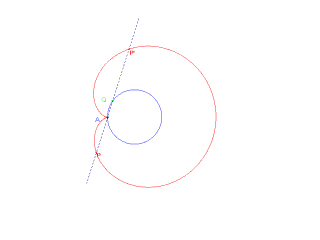
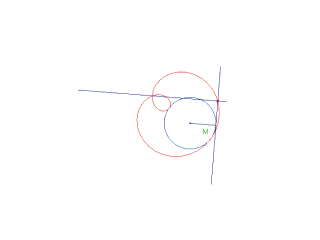
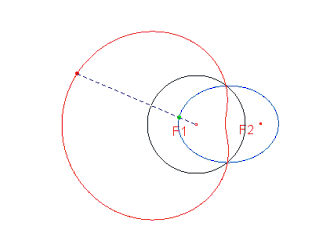
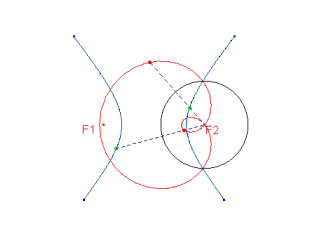
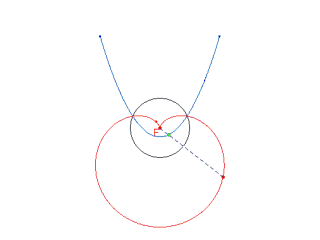
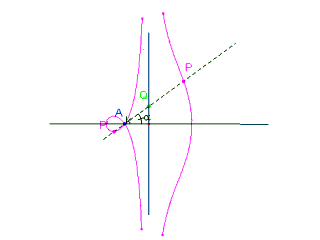
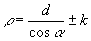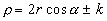Se "C" è una curva qualsiasi e A è un punto fisso,
su una retta per A, che intesechi la curva "C" in Q, si determinino due punti P e P' tali che QP=QP'=k (costante). Il luogo dei punti P e P' si chiama concoide di base "C", polo A, intervallo k.
1° caso:
la base è una retta, il polo non appartiene alla retta. Si ha allora una Concoide di Nicomede.
Indichiamo con d la distanza tra il polo e la retta: la concoide è costituita da due rami separati, uno dei quali ha in A un nodo, una cuspide o un punto isolato a seconda che k > d, k = d, k < d. La curva si può facilmente tracciare con buona precisione. Per questo Newton propose di inserirla, insieme alla retta e alla circonferenza, fra le curve "di servizio": fra quelle cioè che il geometra è "autorizzato" a impiegare in ogni occasione (CFR. Aritmetica Universale, ed. Beaudeux, Parigi 1802, tomo II, pag. 52).
Equazione polare: 
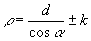
Vedi modelli:
Generazione di quartiche : concoide della retta (metodo di Nicomede). Generazione di quartiche : concoide della retta (metodo del Suardi). Generazione di quartiche : concoide della retta (metodo di Cartesio).
2° caso:
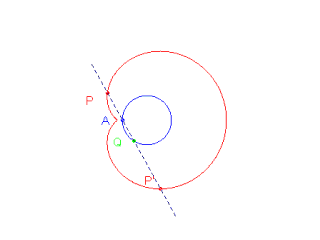
La base Euna circonferenza, il polo appartiene alla circonferenza. Si ha allora una Lumaca del Pascal. Indichiamo con r il raggio della circonferenza: la curva è costituita da un unico ramo che presenta:
 |
|
un punto isolato se k>2r.
|
 |
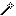
Nel caso k = 2r la curva è nota col nome di Cardioide.
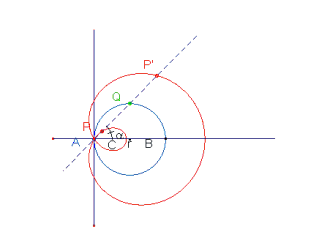Equazione polare: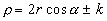 
Notevoli i seguenti teoremi:
|
"Le lumache del Pascal sono podarie di una circonferenza rispetto a un punto del suo piano."
|
|
"Le lumache del Pascal sono trasformate di una conica in una inversione circolare che abbia come centro un fuoco della conica."
|
|
"Una circonferenza (variabile) avente come diametro il segmento che unisce un punto fisso a un punto (variabile) di una circonferenza prefissata, inviluppa una lumaca del Pascal."
|
|
"Se k = r la lumaca corrispondente (dotata di nodo) è una trisettrice."
|
Vedi modelli:
Movimento dei due piani.
Generazione di quartiche: lumache del Pascal.
Generazione di sestiche: concoide della circonferenza (Suardi).
|
