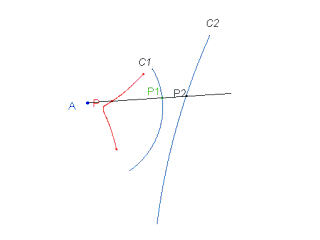
Date in un piano due curve qualsiasi "C1" e "C2" ed un punto fisso A, si conduca per A una trasversale arbitraria che intersechi quelle curve rispettivamente in "P1" e "P2"; sulla trasversale si determini un punto P tale che sia (in valore assoluto e nel verso che procede dalla prima alla seconda curva) AP=P1P2: il luogo dei punti P si chiama Cissoide rispetto al polo A delle curve base "C1" e "C2". Si noti che le curve base possono coincidere in un置nica curva "C": la trasversale per A dovrà allora intersecare tale curva base in due punti distinti "P1" e "P2" (per il resto la definizione rimane immutata: si noti tuttavia che non potendosi in tal caso definire il verso del segmento AP perchè i punti "P1" e "P2" si possono considerare appartenenti ad entrambe le curve, tale segmento va riportato sia dall置na che dall誕ltra parte di A).
1° caso:
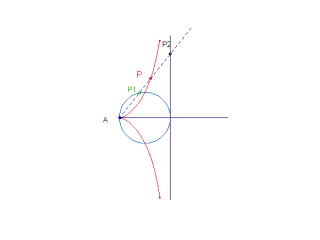
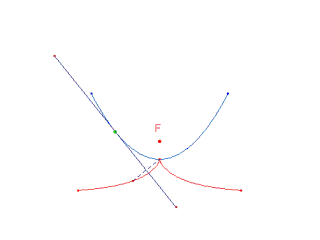
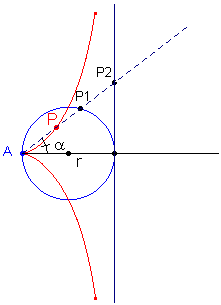
le curve base sono una circonferenza e una sua tangente, il polo è il punto della circonferenza diametralmente opposto al punto di tangenza: si ha allora una Cissoide di Diocle.
È una cubica, dotata di cuspide nel polo. Indichiamo con r il raggio della circonferenza base: dalla figura seguente si ricava facilmente l'equazione polare:  .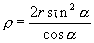
Notevoli i seguenti teoremi:
|
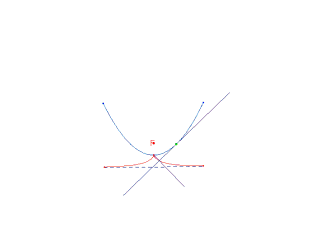
"La podaria di una parabola rispetto al suo vertice è una cissoide di Diocle".
|
|
"Il luogo dei punti simmetrici del vertice di una parabola rispetto alle tangenti alla stessa è una cissoide di Diocle"
|
|
"Se una parabola ruzzola (senza strisciare) su una parabola uguale toccandola
sempre esternamente, il vertice di essa descrive una cissoide di Diocle"
|
 Vedi modelli:
parabole che rotolano l置na sull誕ltra senza strisciare;
Generazione di cubiche: squadra di Newton;
Generazione di cubiche: cissoide (metodo del Suardi).
2° caso:
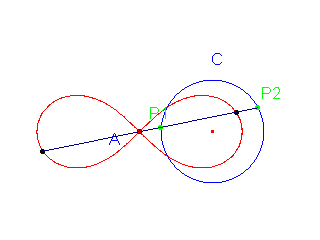
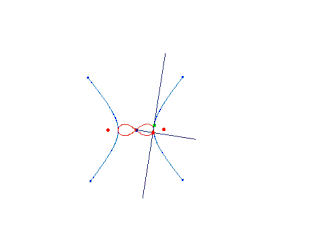
le curve base coincidono in un置nica circonferenza di raggio r; il polo è nel piano della circonferenza, a distanza dal centro uguale a 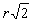 : si ha allora una Lemniscata del Bernoulli.
È una quartica bicircolare nodata. Si ricava
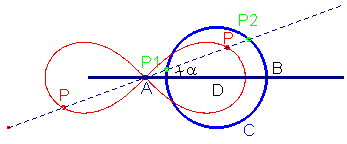essendo r = DB e  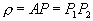la equazione polare:  .
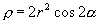Notevoli i seguenti teoremi:
|
"La lemniscata è la podaria di una iperbole equilatera rispetto al centro di questa."
|
|
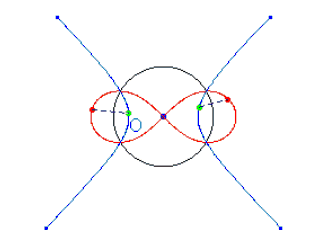
"La lemniscata si ottiene assoggettando una iperbole equilatera ad una inversione circolare il cui polo cade nel centro dell段perbole."
|
|
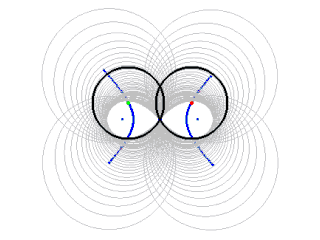
"La lemniscata si può ottenere come inviluppo di una famiglia di circonferenze i cui centri siano punti di una iperbole equilatera, e i cui raggi siano uguali alla distanza di questi punti dal centro dell段perbole."
|
Osserviamo anche: la lemniscata del Bernoulli rientra, come caso particolare, fra le Curve del Cassini, che a loro volta sono particolari Spiriche.
Vedi modelli:
generazione di quartiche: lemniscata del Bernoulli ;
Generazione di quartiche: sezioni del toro (metodo del Delaunay).
|
