丂
丂丂側偤丆偙偺傛偆側婍嬶乮偟偔傒乯偱丆懭墌偑昤偗傞偺偱偟傚偆偐丏偦偺偙偲偵偮偄偰峫偊偰傒傑偟傚偆丏
丂懭墌偺惈幙偼條乆偁傝傑偡偑丆偙偙偱偼丆掕墌廃忋偺摨揰俹偐傜丆偦偺墌偺掕捈宎偵悅慄傪堷偒丆俹俵傪堦掕偺斾偵奜暘乮傑偨偼撪暘乯偡傞揰倃偺婳愓偑懭墌偲側傞偙偲傪棙梡偟偰丆偙偺婍嬶傪峫偊偨傛偆偱偡丏
丂偱偼丆Cavalieri偺婍嬶偺応崌丆偙偺惈幙偑棙梡偝傟偰偄傞偐妋偐傔偰傒傑偡丏
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂
丂
丂慄暘倁俼傪捈宎偲偡傞墌傪昤偒丆偙偺墌偲慄暘俛俠偲偺岎揰傪俽偲偟傑偡丏
丂峏偵丆倁俿丆倁俼丆俻俫乮亖HA乯偺挿偝傪倢丆倣丆![]() 偲偟傑偡丏
偲偟傑偡丏
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂佢俿倁俼亖佢俼亖佢俻俫俼
丂佢倁俼俿亖佢俫俼俻丂丂丂傛傝
丂丂丂丂儮俿倁俼佷儮俻俫俼
丂丂丂丂亪俿倁丗倁俼亖俻俫丗俫俼
丂丂丂丂丂丂倢丗丂倣亖![]() 丂丗俫俼
丂丗俫俼
丂丂丂丂丂亪丂俫俼丂亖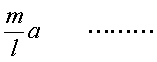 嘆
嘆
丂嘆傛傝丆倁俫亖倁俼亅俫俼
丂丂丂丂丂丂丂亖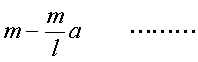 嘇
嘇
丂佢倁俹俙亖佢倁俫俹亖佢俹俫俙亖佢俼傛傝
丂丂丂丂丂儮倁俫俹佷儮俹俫俙
丂丂丂丂丂亪倁俫丗俫俹亖俹俫丗俫俙
丂嘇傛傝丆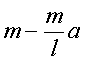 丗俫俹亖俹俫丗
丗俫俹亖俹俫丗![]()
丂丂丂丂丂丂丂俫俹丒俹俫亖乮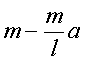 乯
乯![]()
丂丂丂丂丂丂丂丂丂俫俹![]() 亖
亖![]() 乮
乮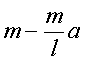 乯
乯![]()
丂俫俹>侽傛傝丆丂俫俹亖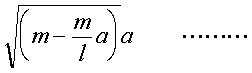 嘊
嘊
丂揰俽偼丆慄暘倁俼傪捈宎偲偡傞墌偺墌廃忋偺揰偱偁傞偐傜丆
丂丂丂丂丂丂丂佢倁俽俼亖佢俼
丂傑偨丆佢倁俫俽亖佢俼亖佢俽俫俼傛傝
丂丂丂丂丂丂丂儮倁俫俽佷儮俽俫俼
丂丂丂丂丂丂丂亪倁俫丗俫俽亖俽俫丗俫俼
丂嘆丆嘇傛傝丆乮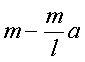 乯丗俫俽亖俽俫丗
乯丗俫俽亖俽俫丗![]()
丂丂丂丂丂丂丂丂丂丂俫俽丗俽俫亖乮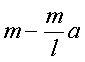 乯
乯![]()
丂丂丂丂丂丂丂丂丂丂丂丂俫俽![]() 亖乮
亖乮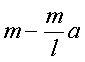 乯
乯![]()
丂俫俽>侽傛傝丆丂俫俽亖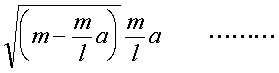 嘋
嘋
丂嘊丆嘋傛傝丆俫俽丗俫俹亖 丗
丗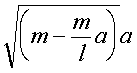
丂丂丂丂丂丂丂丂丂丂丂丂亖![]() 丗侾
丗侾
丂傛偭偰丆慄暘倁俼傪捈宎偲偡傞墌偐傜丆慄暘倁俼偵壓傠偟偨悅慄傪![]() 丗侾偵奜暘偡傞揰偺婳愓偑Cavalieri偺婍嬶偵傛偭偰昤偐傟傞懭墌偲偄偆偙偲偵側傝傑偡丏
丗侾偵奜暘偡傞揰偺婳愓偑Cavalieri偺婍嬶偵傛偭偰昤偐傟傞懭墌偲偄偆偙偲偵側傝傑偡丏
丂廬偭偰丆Cavalieri偺婍嬶偺傛偭偰昤偐傟傞懭墌偼丆倢偲倣丆懄偪倁俿偲倁俼偺挿偝偵傛偭偰掕傑傞偙偲偵側傝傑偡丏丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮廔乯
悢妛幚尡幒傊
偄傠偄傠側婡峔偲悢妛幚尡僩僢僾傊
悢妛偺楌巎攷暔娰