| 帰結 |
パスカルは、その著書『数三角形論』のなかで、数三角形に関する種々の性質を「帰結」としてまとめており、その数は19個にも及ぶ。なかでも、12番目の帰結の証明には数学的帰納法の原型とも言える証明論法が用いられており、これはパスカルの業績の一つと言える.
以下に「帰結第12」とパスカルによるその証明について見る。 |
| 帰結第12 |
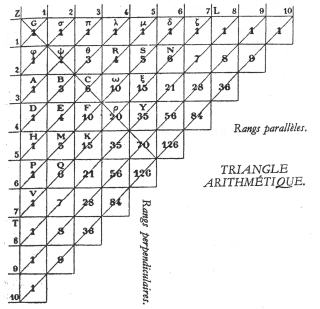
あらゆる数三角形において、同じ底辺にあって隣接する2つの細胞のうち、上位の細胞と下位の細胞との比は、上位の細胞から底辺の最上段までの細胞の個数(両端の細胞を含む)と、下位の細胞から最下段までの細胞の個数(両端の細胞を含む)との比に等しい。
<パスカルによる証明>
この命題には無限に無限に多くの場合があるが、私は2つの補題を仮定することによって、きわめて短い証明を与えよう。
第1.これは自明であるが、この比例は第2底辺において成り立つ。なぜならばφとσとの比が1と1との
比に等しいことは極めて明らかである。
第2.もしこの比例が任意の1底辺において成り立つならば、それは必然的に次の底辺においても成
り立つ。
ここから、この比例が必然的にすべての底辺において成り立つことがわかる。なぜならば、補題1によって、この比例は第2底辺において成り立つ。故に、補題2によって、それは第3底辺において成り立つ。故に、第4底辺においても成り立つ。以下限りなく同様である。
故に、補題2のみを証明すればよい。それには次のようにする。いま、この比例が任意の1底辺、例えば第4底辺Dλにおいて成り立つとする。すなわち、DとBとの比が1と3との比に、Bとθとの比が2と2との比に、θとλとの比が3と1との比にそれぞれ等しいとする。そうすれば、同じ比例が次の底辺Hμにおいても成り立ち、例えばEとCとの比は2と3との比に等しい。
なぜならば、仮定によって、DとBとの比は1と3との比に等しい。
故に、D+BとBとの比は1+3と3との比に等しい。
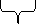 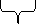
E とBとの比は 4 と3との比に等しい。
同様に、仮定によって、Bとθとの比は2と2との比に等しい。
故に、B+θとBとの比は2+2と2との比に等しい。
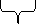 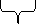
C とBとの比は 4 と2との比に等しい。
しかるに、BとEとの比は3と4との比に等しい。
故に、複合比によって、CとEとの比は、3と2との比に等しい。証明終。
|
| 参考文献 |
Blaise Pascal(1954). Trait du
Triangle Arithmetique. OEuvres completes. Gallimard.
ブレーズ・パスカル(1959).
数三角形論(原享吉 訳).
伊吹武彦 ほか (編),
パスカル全集
第一巻(pp.724-735). 人文書院.
ロシュディー・ラーシェド(2004).
アラビア数学の展望(三村太郎
訳). 東京大学出版会.
|
|
|