| パスカルの数三角形 |
 |
| 解 説 |
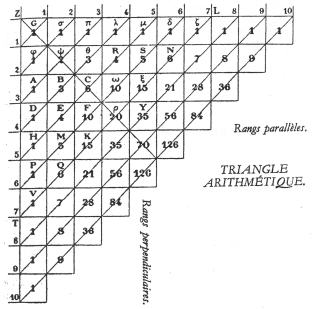
パスカルが考案した数三角形(上図)は、現在我々が教科書で見るような数三角形とは形がことなる。様々な部分に名称が付けられているので紹介する。まず、マス一つひとつを<細胞>と呼ぶ。細胞の一部にはAやYなどの名前が付けられている。これはこの後の数三角形に関する議論をしやすくするためにあると考えられる。ここで、細胞Gは<母細胞>と呼ばれ、Gから縦横均等に10個に分けられている。そして、上部と左部に付けられた1から10までの数字を<分割の指数>と呼ぶ。また、左から右へ進む2つの平行線の間の細胞の集まりを同じ<水平行の細胞>といい、その分割の指数が3だった場合、特に第3水平行の細胞と呼ぶ。同様に、上から下へ進む2つの平行線の間の細胞を同じ<垂直行の細胞>といい、その分割の指数が3だった場合、特に第3垂直行の細胞と呼ぶ。さらに、縦横の同じ分割の指数同士を結んだ左下から右上にかけて引かれた斜めの線を<底辺>と呼ぶ。同じ底辺が対角線状に横切っている細胞を同じ<底辺の細胞>といい、その分割の指数が3だった場合、第3底辺の細胞、もしくは、その底辺の最下段と最上段の細胞の名前をとって、底辺Aπという。同じ底辺の細胞で、その両端から等距離にあるものを<相反細胞>と呼ぶ。ここで、母細胞Gとそれぞれの底辺により、三角形が作られる。この三角形の一つひとつを<数三角形>とよぶ。
各細胞の数はその垂直行における直前の細胞の数とその水平行における直前の細胞の数との和に等しい。例えば、細胞Eの数は細胞Bの数と細胞Dの数との和に等しい。それぞれの細胞の数は細胞Gに入れる任意の数(これを母数という)に依存する。原典では、単に「細胞」といって、その細胞の数が意味されることが多い。
ここで、母数を1とすると、だいn+1底辺の細胞の数は最下段から順に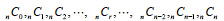 と書ける。 と書ける。
また、「各細胞の数は、その垂直行における直前の数とその水平行における直前の細胞の数との和に等しい」ということは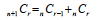 を表していることが分かる。 を表していることが分かる。
参考
|
| 参考文献 |
Blaise Pascal(1954). Trait du
Triangle Arithmetique. OEuvres completes. Gallimard.
ブレーズ・パスカル(1959).
数三角形論(原享吉 訳).
伊吹武彦 ほか (編),
パスカル全集
第一巻(pp.724-735). 人文書院.
|
|
|
|