図２を図４のように数学化し、図３の中心線FEのみに注目し、画面上の原像Xと投象Yの間に潜む関数関係を得れば、原像FXを測定し、関数関係の計算をし、投象（像FY）を目盛つき定規で描画（≠作図）できる。

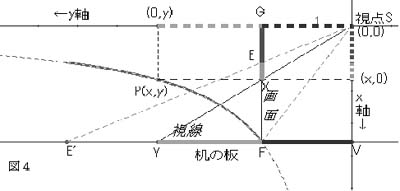
図２で机上に画面FEが垂直に立ち、目の位置、視点Sから画面上の点Ｘをみた際の視線と机の板の交点をＹとし、視点から水平線を眺めた際の視線をｙ軸、ｙ軸と画面の交点をＧ、視点Sから机上へx軸を下ろし、垂線の足をＶとする。三角形の相似に注目すれば、GX：SV＝SG：VY。すなわち、GX×VY＝SV×SG。視点と画面を固定し、視点Sを原点、GX＝xとし、水平線を見込む方向をy軸とみてVY＝ｙとし、長方形SGFVの面積をcとすれば、ｘ×ｙ＝c。VYはGXに反比例し、P(x,y)の軌跡は双曲線の一部となる。奥行きVYがGXに対して反比例するように長さを定めて描画すれば、視点S,原像X、投象Yは視線上に並ぶ。

---

投影とアナモルフォーズの実験室へ戻る
数学の歴史博物館へ戻る

お問い合わせはこちら