アポロニウス以前には、放物線、楕円、双曲線は、それぞれ頂角が直角、鋭角、鈍角である3つの異なる直円錐の切断面として得られていた。約1世紀の間、これらの曲線には発見されたときの方法をそのまま付けただけの呼び方以外に特別な名称はなかった。つまり、「直角円錐の切断面(
orthotome)」「鋭角円錐の切断面(oxytome)」「鈍角円錐の切断面(amblytome)」と呼ばれていた。これらの曲線を、それぞれ放物線(
parabola)、楕円(ellipsis)、双曲線(hyperbola)という名称で呼んだのは、アポロニウスが最初であった。なお、これら3つの用語は、アポロニウスがこのために考えた新しい用語ではない。もともとピタゴラス学派が、それ以前に、二次方程式を面積に当てはめて解こうとしたときに用いられた用語である。元々の意味は、次の通りである。
parabola:過不足しない
ellipsis:不足
hyperbola:超過
つまり、こういうことである。
原点を頂点とする放物線の方程式は
![]()
原点を頂点とする楕円と双曲線の方程式は
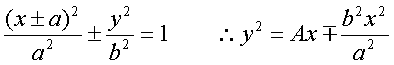
よって楕円は
![]()
双曲線は
![]()
となる。
ゆえに、
y2を正方形の面積、Axを長方形の面積とみなせば、次のような表現が可能になるわけである。放物線 過不足しない(
parabola)楕円 不足(
ellipsis)双曲線 超過(
hyperbola)
数学実験室へ
いろいろな機構と数学実験トップへ
数学の歴史博物館