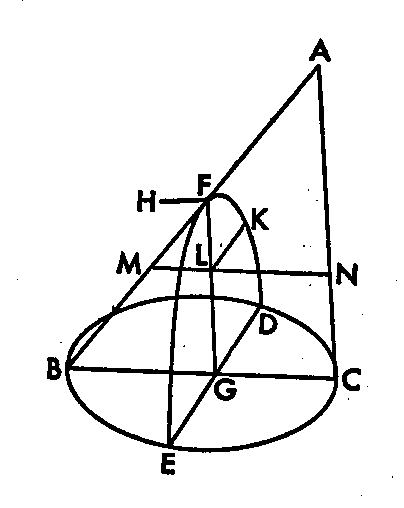
柦戣侾侾丗墌悕偑偦偺幉傪捠傞暯柺偱愗抐偝傟丄幉嶰妏宍偺掙曈偵悅捈側捈慄傪娷傓墌悕偺掙柺傪愗傞暿偺暯柺偱傕愗抐偡傞丅愗抐柺偺墑挿偝傟偨捈宎偑幉嶰妏宍偺曈偺堦偮偵暯峴側傜偽丄墌悕偺愗抐柺偐傜偦偺捈宎偵堷偄偨偳傫側捈慄傕愗抐偡傞柺偲墌悕偺掙柺偺嫟捠晹暘偵暯峴偱丄偦偺暯曽偼丄偦傟偱愗抐偝傟偨愗抐柺偺捀揰偐傜偼偠傑傞捈宎忋偺捈慄偲墌悕偺妏偲愗抐柺偺捀揰偐傜偼偠傑傞捈宎忋偺捈慄偲墌悕偺妏偲愗抐柺偺捀揰娫偺捈慄偵懳偟偰幉嶰妏宍偺掙曈偺暯曽偑嶰妏宍偺巆傝偺俀曈偱嫴傑傟偨挿曽宍偵懳偟偰帩偮斾傪帩偮暿偺捈慄偱嫴傑傟偨挿曽宍偵摍偟偄丅偦偟偰丄偦偺傛偆側愗抐柺傪曻暔慄偲屇傇丅
捀揰偑揰俙偱丄墌俛俠傪掙柺偲偡傞墌悕偑偁傞丅幉傪捠傞暯柺偵傛偭偰愗抐偡傞丅愗抐柺偲偟偰嶰妏宍俙俛俠傪偮偔傞丅乮嘥.3乯偦偟偰丄捈慄俛俠偵悅捈偱丄捈慄俢俤傪娷傒墌悕偺掙柺傪暿偺暯柺偱愗抐偡傞丅墌悕偺昞柺偵愗抐柺偲偟偰嬋慄俢俥俤傪偮偔傞丅愗抐柺偺捈宎俥俧偼幉嶰妏宍偺堦曈俙俠偵暯峴偱偁傞偲偡傞丅乮嘥.7丆掕媊係乯捈慄俥俫偼俥偐傜捈慄俥俧偵悅捈偵堷偔偲偡傞丅偦傟傪丂俛俠俀丗俛俙丒俙俠亖俥俫丗俥俙丂偑惉傝棫偮傛偆偵岺晇偡傞丅
偦偟偰丄擟堄偺揰俲傪愗抐柺忋偵擟堄偵偲傞丅俲傪捠傝丄捈慄俲俴傪捈慄俢俤偵暯峴偵堷偔偲偡傞丅俲俴俀丗亖俫俥丗俥俴丂偲偄偊傞丅
丂偲偄偆偺偼丄捈慄俵俶偼俴傪捠傝丄捈慄俛俠偵暯峴偵堷偔偲偡傞丅捈慄俢俤傕捈慄俲俴偵暯峴偱偁傞丅偦傟備偊偵丄俲俴丄俵俶傪捠傞暯柺偼墌悕偺掙柺偱偁傞俛俠丄俢俤傪捠傞暯柺偵暯峴偱偁傞丅
乮儐乕僋儕僢僪.嘳嘥.15乯偟偨偑偭偰丄俲俴丄俵俶傪捠傞暯柺偼俵俶傪捈宎偲偡傞墌偱偁傞丅乮嘥.4乯偦偟偰丄俲俴偼俢俤偑俛俠偵悅捈偱偁傞偙偲傛傝俵俶偵悅捈偱偁傞丅乮儐乕僋儕僢僪.嘳嘥.10乯
偦傟備偊偵丄俵俴丒俴俶亖俲俴俀丂乮儐乕僋儕僢僪.嘨.31丟嘫.8.宯乯
偦偟偰丄丂丂俛俠俀丗俛俙丒俙俠亖俫俥丒俥俙丂丂
偲丂丂丂丂丂俛俠俀丗俛俙丒俙俠亖乮俛俠丗俛俙乯乮俛俠丗俙俠乯乮儐乕僋儕僢僪 .嘫.23乯
偟偨偑偭偰丂俫俥丗俥俙亖乮俛俠丗俛俙乯乮俛俠丗俙俠乯
偟偐偟丄丂丂俛俠丗俠俙亖俵俶丗俶俙亖俵俴丗俴俥丂乮儐乕僋儕僢僪.嘫.4乯
偦偟偰丄丂丂俛俠丗俛俙亖俵俶丗俵俙亖俴俵丗俵俥亖俶俴丗俥俙丂乮儐乕僋儕僢僪.嘫.2乯
偟偨偑偭偰丂俫俥丗俥俙亖乮俵俴丗俴俥乯乮俶俴丗俥俙乯
偟偐偟丄嫟捠側崅偝偲偟偰捈慄俥俴傪偲傞偲
丂丂丂丂丂丂俫俥丗俥俙亖俫俥丒俥俴丗俴俥丒俥俙丂乮儐乕僋儕僢僪.嘫.1乯
偟偨偑偭偰丄俵俴丒俴俶丗俴俥丒俥俙亖俫俥丒俥俴丗俴俥丒俥俙丂乮儐乕僋儕僢僪.嘪.11乯
偦傟備偊偵丂俵俴丒俴俶亖俲俴俀
偦偺寢壥丂丂俲俴俀亖俫俥丒俥俴
偦偟偰丄偦偺傛偆側愗抐柺傪曻暔慄偲偄偄丄俫俥偼捈宎俥俧偺廲慄曽岦偵堷偐傟偨捈慄偑惓曽宍偵偁偰偼傔傜傟傞捈慄偲偄偄丅偦傟傪捠宎偲傕偄偆丅